Bayesian Optimisation can help Quantum Computing Become a Reality

Quantum computers have the potential to be exponentially faster than traditional computers, revolutionising the way we currently work. While we are still years away from general-purpose Quantum Computing, Bayesian Optimisation can help to stabilise quantum circuits for certain applications. This blog will summarise how Mind Foundry did just that.

Further details feature in this paper, which was submitted to Science. The team was composed of researchers from the University of Maryland, UCL, Cambridge Quantum Computing, Mind Foundry, Central Connecticut State University and IonQ.

The Task

The researchers behind the paper were applying a hybrid quantum learning scheme on a trapped ion quantum computer to accomplish a generative modelling task. Generative models aim to learn representations of data in order to make subsequent tasks easier.

Hybrid quantum algorithms use both classical and quantum resources to solve potentially difficult problems. The Bars-and-Stripes (BAS) data-set was used in the study as it can be easily visualised in terms of images containing horizontal bars and vertical stripes where each pixel represents a qubit.

The experiment was performed on four qubits within a seven-qubit fully programmable trapped ion quantum computer. The quantum circuits are structured as layers of parameterised gates which will be calibrated by the optimisation algorithms. The following figure taken from the paper illustrates the set up.

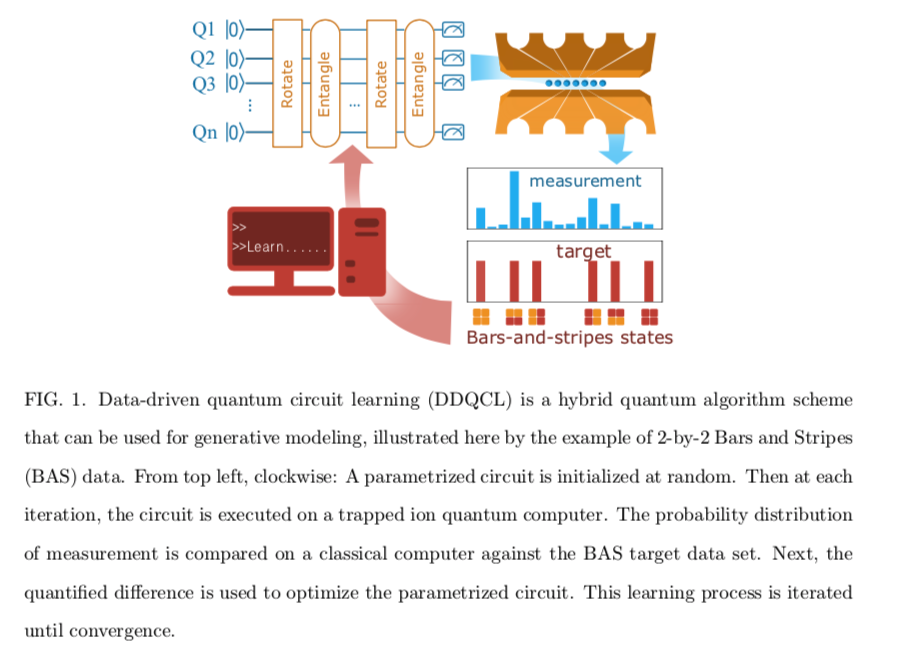
Training the quantum circuit

The researchers used two optimisation methods in the paper for the training algorithm:

• Particle Swarm Optimisation (PSO): a stochastic scheme that works by creating many “particles” randomly distributed across that explore the landscape collaboratively

• Bayesian Optimisation with the Mind Foundry Platform: a global optimisation paradigm that can handle the expensive sampling of many-parameter functions by building and updating a surrogate model of the underlying objective function.

The optimisation process consists in simulating the training procedure for a classical simulator in place of the quantum processor for a given set of parameters.

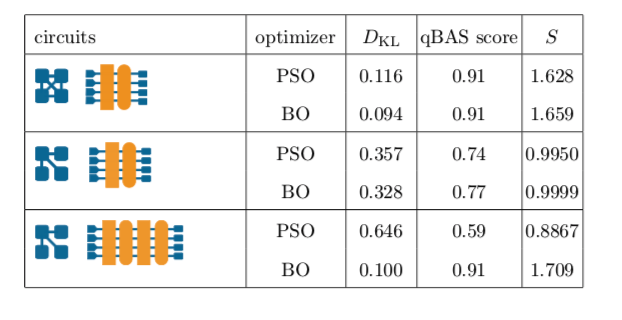
Once the optimal parameters have been identified, the training procedure is then run on the ion quantum computer in Figure 1. The cost functions used to quantify the difference between the BAS distribution and the experimental measurements of the circuit are variants of the original Kullback-Leibler Divergence and are detailed in the paper.

Results and outlook

The training results for PSO and Mind Foundry Optimise are provided in the following figures:

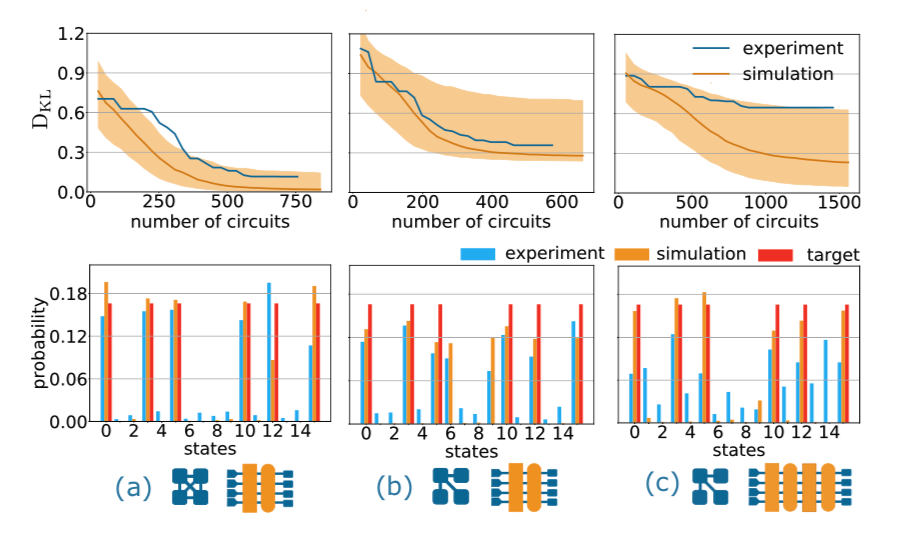
Quantum circuit training results with PSO

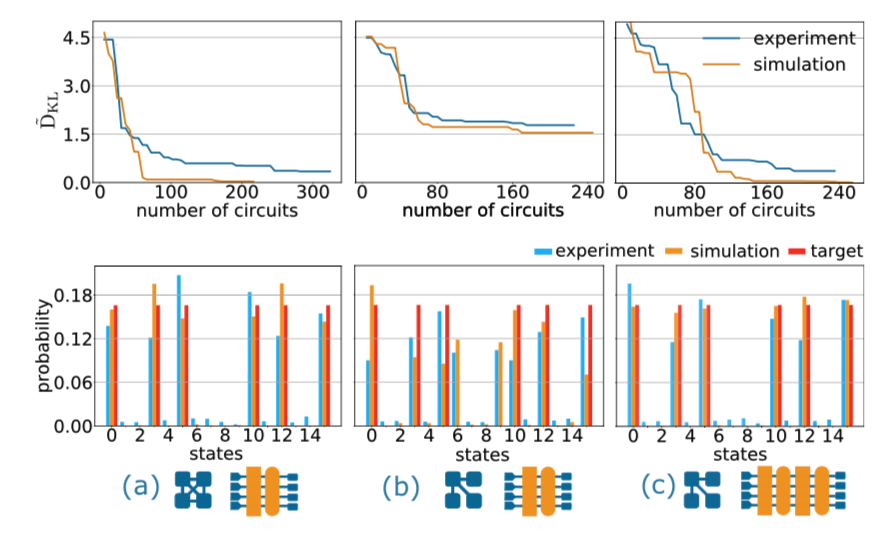
Quantum circuit training results with the Mind Foundry Platform

The simulations are in orange and the ion quantum computer results are in blue. Column (a) corresponds to a circuit with two layers of gates and all-to-all connectivity. Columns (b) and (c ) correspond to a circuit with two and four layers and start connectivity, respectively. (a), (b) and (c ) have 14, 11 and 26 tuneable parameters respectively.

We observe that the circuit is able to converge well to produce the BAS distribution only for the first circuit with PSO whereas with Mind Foundry Optimise all circuits are able converge. According to the researchers, the success of Mind Foundry Optimise on the 26 parameter circuit represents the most powerful hybrid quantum application to date.